Overview of QUA¶

A QUA program defines the sequence of:

Pulses sent to the quantum device
Measurements of pulses returning from the quantum device
Real-time classical calculations done on the measured data
Real-time classical calculations done on general classical variables
Real-time decision making that affects the flow of the program.

In addition to the specification of which pulses are played, it also specifies when they should be played through both explicit and implicit statements and dependency constructs. Thus, a QUA program also defines exactly the timing in which pulses are played, down to the single sample level.

The pulses syntax defines an implicit pulse dependency, which determines the order of pulse execution. The dependency can be summarized as follows:

Each pulse is played immediately, unless dependent on a previous pulse
Pulses applied to the same quantum element are dependent on each other according to the order in which they are written in the program

We first describe in detail the pulses and measurement statements and their relation to the configuration and then list and specify all of the language statements and data types.

Playing Pulses and Performing Measurements in QUA¶

Play Statement
Analog Waveform Manipulations
- Single Input Element
- Mixed Inputs Element
Digital Waveform Manipulations
The C Matrix
Frequency and phase transformations
Amplitude transformations
- The single tone case
Measure statement
Multiple OPX timing and latencies

QUA is a pulse-level-control programing language for quantum devices. This means that it allows programmers to control the shapes and timing of the pulses that are sent to the quantum elements in the quantum device. This enables programmers to perform the operations on them, as well as the timing and parameters of the measurement operations done on signals that return from the quantum elements. Thus, the most basic statements in QUA are play statement and the measure statement.

Play Statement ¶

The most basic statement in QUA is the play statement:

play(pulse, element)

This statement instructs the OPX to send the indicated pulse to the indicated element. Importantly, the OPX will modify or manipulate the pulse according to the element’s properties defined in the configuration.

Analog Waveform Manipulations ¶

Single Input Element ¶

If the element has a single input, the pulse sent to it must be defined with a single waveform. For example:

'elements': {
    'qubit': {
        'SingleInput': {
            'port': ('con1', 1),
            },
            'intermediate_frequency': 70e6,
            'operations': {
                'pulse1': 'pulse1'
            },
        },
    },
    'pulses': {
        'gauss_pulse_in': {
            'operation': 'control',
            'length': 12,
            'waveforms': {
                'single': 'wf1',
            },
        }
    },
    'waveforms': {
        'wf1': {
            'type': 'arbitrary',
            'samples': [0.49, 0.47, 0.44, ...]
        },
    }

Let us denote the samples of the waveform by \(s_i\). The play statement instructs the OPX to modulate the waveform samples with the intermediate_frequency of the element:

\[\tilde{s_i} = s_i \cos(\omega_{IF} t + \phi_F),\]

where \(\omega_{IF}\) is the intermediate frequency defined in the configuration of the element and \(\phi_F\) is the frame phase, initially set to zero (see z_rot() statement specifications in QUA Language DSL Reference for information on \(\phi_F\) ). The OPX then plays \(s_i\) to the analog output port defined in the configuration of the element (in the above example, port 1).

Mixed Inputs Element ¶

If the element has two mixed inputs (i.e. two output ports of the OPX are connected to the element via an IQ mixer), in addition to the intermediate frequency, a mixer and a lo_frequency are defined in the configuration. For example:

'elements': {
                'qubit': {
                        'mixedInputs': {
                                'I': ('con1', 1),
                                'Q': ('con1', 2),
                                'mixer': 'mixer1',
                                'lo_frequency': 5.1e9,
                        },
                        'intermediate_frequency': 70e6,
                        'operations': {
                                'pulse1': 'pulse1'
                        },
                },
},

A pulse that is sent to such element must be defined with two waveforms. For example:

'pulses': {
                'pulse1': {
                        'operation': 'control',
                        'length': 12,
                        'waveforms': {
                                'I': 'wf_I',
                                'Q': 'wf_Q',
                        },
                },
        },
'waveforms': {
                'wf_I': {

                        'type': 'arbitrary',
                        'samples': [0.49, 0.47, 0.44, ...]
                },
                'wf_Q': {
                        'type': 'arbitrary',
                        'samples': [-0.02, -0.03, -0.03, ...]
                },
}

In addition, a mixer must be defined with a mixer correction matrix that corresponds to the intermediate_frequency and the lo_frequency. For example:

'mixers': {
                'mixer1': [
                        {'intermediate_frequency': 70e6,
                        'lo_frequency': 5.1e9,
                        'correction': [0.9, 0.003, 0.0, 1.05]}
                ],
}

Denoting the samples of the waveforms by \(I_i\) and \(Q_i\), the play statement instructs the OPX to modulate the waveforms samples with the intermediate frequency of the element and to apply the mixer correction matrix in the following way:

(1)¶\[\begin{split}\begin{pmatrix} \tilde{I_i} \\ \tilde{Q_i} \end{pmatrix} = \begin{pmatrix} C_{00} & C_{01}\\ C_{10} & C_{11} \end{pmatrix} \begin{pmatrix} \cos(\omega_{IF}t+\phi_F) & -\sin(\omega_{IF}t+\phi_F)\\ \sin(\omega_{IF}t+\phi_F) & \cos(\omega_{IF}t+\phi_F) \end{pmatrix} \begin{pmatrix} I_i \\ Q_i \end{pmatrix}\end{split}\]

where \(\omega_IF\) is the intermediate_frequency, and the \(C_{ij}\)’s are the matrix elements of the correction matrix defined in the mixer for the relevant intermediate_frequency and lo_frequency. As mentioned above, \(\phi_F\) is the frame phase, initially set to zero (see frame_rotation() statement specifications in QUA Language DSL Reference for information). The OPX then plays \(I_i\) and \(Q_i\) to the analog output ports defined in the configuration of the element (in the above example, port 1 and port 2, respectively).

Digital Waveform Manipulations ¶

To understand how digital signals are treated, we concider the following example where we output an analog signal through a switch. There is now one analog input to the quantum element, from which the analog waveform is played, and one digital input which is used to open the switch. The signal is then collected via switch and a quantum element output as is shown in the figure below.

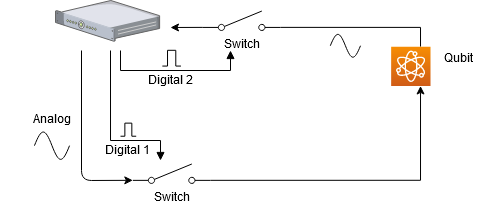
There is some propagation delay during which the signal travels down the wire from the OPX and toward the switch. We therefore want to delay the digital signal such that the switch transmits during the correct window. Additionally, there may be some dispersion broadening the analog pulse and we may want to take this effect into account. QUA allows us to do both these things, as we are about to see. Because they are associated with the physical configuration of connections to the device (wire lenghts, resonator ring up times etc) they are part of the quantum element configuration.

Configuration ¶

To define a digital input of a quantum element the configuration must have the following three properties: port, delay, and buffer. delay represents the signal propagation time and buffer defines the broadening of the signal. It is a symmetrical window before and after the analog pulse. Both parameters are in units of ns. Configuration is done as follows:

'elements': {
                'qubit': {
                        'mixedInputs': {
                                'I': ('con1', 1),
                                'Q': ('con1', 2),
                                'mixer': 'mixer1',
                                'lo_frequency': 5.1e9,
                        },
                        'intermediate_frequency': 70e6,
                        'digitalInputs':{
                                'digital_input1':{
                                         'port': (cont1, 1),
                                         'delay': 144,
                                         'buffer': 8,
                                         },
                                'digital_input2':{
                                         'port': (cont1, 2),
                                         'delay': 88,
                                         'buffer': 20,
                                         }
                                        },
                        'operations': {
                                'pulse1': 'pulse1'
                        },
                },
}

Defining a pulse ¶

A pulse that is played to a quantum element with a digital input, can include a single digital marker which points to a single digital waveform. For example:

'pulses': {
                'pulse1': {
                        'operation': 'control',
                        'length': 40,
                        'waveforms': {
                                'I': 'wf_I',
                                'Q': 'wf_Q',
                        },
                   'digital_marker': 'digital_waveform_high'
                },
        },
'digital_waveforms': {
                'digital_waveform_high': {
                        'samples': [(1, 0)]
                },
}

The coding of the digital waveform is a list of the form: [(value, length), (value, length), …, (value, length)], where each value is either 0 or 1 indicating the digital value to be played (digital high or low). Each length is an integer (divisible by 4) indicating for how many nanoseconds the value should be played. A length 0 indicates that the corresponding value is to be played for the remaining duration of the pulse. In the example above, the digital waveform is a digital high.

When such pulse is played to the element, via the play or the measurement command, the digital waveform is sent to all the digital inputs of the element. For each digital input, however, the OPX:

Delays the digital waveform by the delay that is defined in the configuration of the digital input (given in ns).
Convolve the digital waveform with a digital pattern that is high for a duration which is twice the buffer that is defined in the configuration of the digital input (given in ns).
Plays the digital waveform to the digital output of the OPX that is indicated is defined in the configuration to be connected to the digital input.

In the example above a play(pulse1, qubit) command would play:

A digital waveform to digital output 1, which starts immediately after the analog waveforms (due to an intrinsic time delay of the analog channel with respect to the digital channel), and which is high for 56 ns (the length of the pulse plus 2x8 ns).
A digital waveform to digital output 2, which starts 64 ns before the analog waveforms and which is high for 80 ns (the length of the pulse plus 2x20 ns).

Digital markers and quantum element readout ¶

The output of a quantum element can be read by the OPX. Returning to the example we considered above, the same effects of delay and dispersion will affect the readout. For this reason we configure the time-of-flight and smearing parameters, which are identical to the delay and buffer we defined above, but for the case of element output. This is discussed in detail in the Demodulation and Measurements section. The digital waveform used to define this behaviour is called a digital marker and is a part of the way the OPX performs a raw ADC stream readout. When a digital marker is not defined, a raw ADC stream will be measured as a list of zeros. This is a common pitfal when taking raw analog data. We emphasize this point:

Warning

Even if a measurement is performed without the need of a digital channel, a digital marker MUST be defined if an ADC stream is required.

The C Matrix ¶

Just before a pulse leaves the pulse processor, it is multiplied by the C (correction) matrix.

The C matrix is a 2x2 transformation matrix multiplying the (I, Q) vector coming out of the pulse generator in order to generate the final output (I,Q) waveform:

\[\begin{split}\begin{pmatrix} I' \\ Q' \end{pmatrix} = C \begin{pmatrix} I \\ Q \end{pmatrix}\end{split}\]

Where the matrix is:

\[\begin{split}C = \begin{pmatrix} C_{II} & C_{IQ} \\ C_{QI} & C_{QQ} \end{pmatrix}\end{split}\]

The C matrix is an arbitrary correction matrix to the [I,Q] vector supplied by the user. The matrix values can be updated for each element either during the configuration stage via the ‘correction’ parameter in the ‘mixers’ construct:

'mixers': {
    'mixer1': [
        {
            'intermediate_frequency': 70e6,
            'lo_frequency': 5.1e9,
            'correction': [0.9, 0.003, 0.0, 1.05]
        }
    ],
}

or later on as part of a program using the update_correction() function:

# updating the C matrix associated with element_1
update_correction('element_1', C_II, C_IQ, C_QI, C_QQ)

The dynamic correction parameters can of course be calculated in real time, based on, for example, the outcome of measurements.

Frequency and phase transformations ¶

In this section we describe how to control the frequency/phase matrix in Eq. (1).

Updating \(\omega_{IF}\)

The frequency associated with an element can be updated using the update_frequency() function in the following way:

# update frequency of element_1 to 10 MHz
update_frequency('element_1', 10e6)
# update frequency of element_1 with the value stored in the variable frequency
update_frequency('element_1', frequency)
# update the frequency with a continuous phase transition
update_frequency('element_1', frequency, keep_phase=True)

Note

Phase behavior of update_frequency

By default (keep_phase=False), The phase of the signal after the frequency has been updated is consistent with a change of \(\omega_{IF}\) only as defined in eq. (1). Namely, if the phase \(\omega_{IF}t\) will change according to the rule

\[\omega_1 t_0 \rightarrow \omega_2 (t_0+\Delta t)\]

where \(\omega_1\), \(\omega_2\) are the frequencies before and after the transition, \(\Delta t\) is the sampling rate and \(\rightarrow\) signifies a transition from the sample \(t_0\) to the next.

To maintain a continuous phase through the transition, use keep_phase=True. This will update the phase the phase accodring to the rule

\[\omega_1 t \rightarrow \omega_1 t + \omega_2 \Delta t.\]

Updating \(\phi_{F}\)

Adding a fixed phase to the [I,Q] vector is possible using the frame_rotation():

# setting the phase of element_1 to pi
frame_rotation(np.pi, 'element_1')

# setting the phase of element_1 to the value stored in variable phi
phi = declare(fixed)
assign(phi, pi)
frame_rotation(phi, 'element_1')

Please note that using a variable can have a larger overhead compared to using a fixed number. If the real time requirements are strict, consider pre-calculating the phases and merging frame_rotation() calls whenever possible.

Resetting \(\omega_{IF}t\)

One can reset the phase associated with a frequency using reset_phase():

# resetting the phase of element_1
reset_phase('element_1')

Note

Reset phase will only reset the phase of the intermediate frequency (\(\omega_{IF}\)) currently in use.

Resetting \(\phi_{F}\)

To reset the frame, the reset_frame() command can be used:

# setting F to be the identity matrix (phi=0)
reset_frame('element_1')

Amplitude transformations ¶

Pulses can be amplitude modulated via the amp() parameter inside a play() command:

play(pulse*amp(A), element)

Where A can be either a number or a matrix in the case of [I,Q] modulations. Notice that amp() operates on the pulses whereas functions such as frame_rotation() or update_frequency() operate on elements instead.

The single tone case ¶

In case only a single tone is played (not in an I/Q configuration), the C transformation no longer exists and amplitude manipulations are done simply via the amp() parameter inside a pulse command:

Measure statement ¶

The measurement statement is the most complex statement in QUA, and looks like this:

measure(pulse, element, stream_name, (integration_weights, variable), (integration_weights, variable))

It can only be done for an element that has outputs defined in the configuration. For example:

'elements': {
                'resonator': {
                        'mixedInputs': {
                                'I': ('con1', 3),
                                'Q': ('con1', 4),
                                'mixer': 'mixer1',
                                'lo_frequency': 7.3e9,
                        },
                        'intermediate_frequency': 50e6,
                        'outputs': {
                                'out1': : ('con1', 1),
                        },
                        'time_of_flight': 196,
                        'smearing': 20,
                },
}

As seen in this example, when a quantum element has outputs, two additional properties must be defined: time_of_flight and smearing. The pulse used in a measurement statement must also be defined as a measurement pulse and must have have integration_weights defined. For example:

'pulses': {
                'pulse1': {
                        'operation': 'measurement',
                        'length': 400,
                        'waveforms': {
                                'I': 'meas_wf_I',
                                'Q': 'meas_wf_Q',
                        },
                   'integration_weights': {
                                'integ1': 'integW1',
                                'integ2': 'integW2',
                        }
'integration_weights': {
                'integW1': {
                        'cosine': [0.0, 0.5, 1.0, 1.0, ..., 1.0, 0.5, 0.0]
                        'sine': [0.0, 0.0, ..., 0.0]
                },
                'integW2': {
                        'cosine': [0.0, 0.0, ..., 0.0]
                        'sine': [0.0, 0.5, 1.0, 1.0, ..., 1.0, 0.5, 0.0]
                },
}

A measurement statement, such as the one shown above, instructs the OPX to:

Send the indicated pulse to the indicated element, manipulating the waveforms in the same manner that is described in the play statement section above.
After a time period time_of_flight (given in ns), samples the returning pulse at the OPX input port/s that are connected to the output/s of the element. It saves the sampled data under stream_name (unless stream_name = None, in which case the sampled data will not be saved). The sampling time window will be of a duration that is the duration of the pulse plus twice the smearing (given in ns). This accounts for the returning pulse that is longer than the sent pulse due to the response of the quantum device, as well as for the cables and other elements in the pulse’s path.
Demodulate the sampled data with a frequency intermediate_frequency, defined in the configuration of the element, perform weighted integration on the demodulated data with integration_weights that are defined in the configuration, and put the result in the indicated variable. The OPX can perform 10 demodulations and integrations at any given point in time, which may or may not be a part of the same measurement statement. The precise mathematical operation on the sampled data is:

\[\mathrm{variable} = \sum_i s_i \left[ w_c^i \cos(\omega_{IF} t_i + \phi_F) + w_s^i\sin(\omega_{IF} t_i + \phi_F)\right]\]

where \(\omega_{IF}\) corresponds to intermediate_frequency, \(\phi_F\) is the frame phase discussed above, and \(w_c^i\) and \(w_s^i\) are the cosine and sine integration_weights, respectively.

Note

The integration_weights are defined in a time resolution of 4 ns, while the sampling is done with time resolution of 1 ns (1GSa/sec sampling rate):

\[w_{c/s}^{4i} = w_{c/s}^{4i} + w_{c/s}^{4i+1} + w_{c/s}^{4i+2} + w_{c/s}^{4i+3}\]

Multiple OPX timing and latencies ¶

When operating with multiple controllers, an additional latency due to communication overhead will occur. This happens in two cases:

When aligning two quantum elements which are on separate controllers, and it is impossible for the compiler to determine how long each of the elements will need to wait for the other (for example, due to a branching in the code)
When performing a measurement on a quantum element in one controller and using the result of that measurement to affect the playing of a quantum element in a different controller.

When transferring arrays, the latency will also increase with the length of the array.